Как найти параллельное сопротивление

При работе с электрическими цепями сопротивление играет важную роль в определении тока и напряжения в системе. В данной статье мы рассмотрим, как найти параллельное сопротивление в электрических цепях. Мы разберем основные концепции и предоставим полезные советы для упрощения расчетов.

Сопротивление в последовательной цепи

Перед тем как перейти к параллельным цепям, давайте кратко вспомним о сопротивлении в последовательной цепи. В последовательной цепи резисторы соединены так, что ток проходит через каждый из них последовательно. Общее сопротивление такой цепи можно вычислить, просто сложив значения сопротивлений каждого резистора.

Сопротивление при параллельном соединении

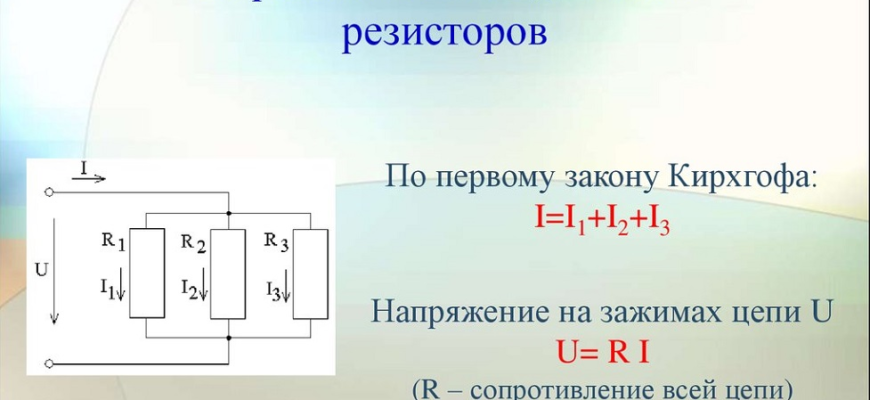
В случае параллельного соединения резисторов ситуация несколько иная. Здесь ток разделяется между резисторами, и напряжение на каждом из них одинаково. Чтобы найти общее параллельное сопротивление, следует использовать следующий метод:

1. Обратные величины: Начните с вычисления обратных величин каждого сопротивления (1/R). Для этого вам понадобится калькулятор.
2. Сумма обратных величин: Сложите все обратные величины (1/R1 + 1/R2 + 1/R3 + …).
3. Обратное от суммы: Полученную сумму обратных величин снова возьмите в обратное (1/сумма).
4. Получение общего сопротивления: Теперь, имея обратное значение, найденное на предыдущем шаге, возьмите его обратное значение, чтобы получить общее параллельное сопротивление (Rпараллельное).

Полезные советы

• Если вам нужно найти сопротивление только двух резисторов, формула может быть немного упрощена: Rпараллельное = (R1 * R2) / (R1 + R2).
• Если в цепи присутствует более двух резисторов, продолжайте добавлять обратные величины и следуйте вышеуказанным шагам.
• При работе с параллельными цепями всегда следите за единицами измерения сопротивлений. Убедитесь, что все сопротивления измерены в одних и тех же единицах (обычно Ом).
• Не забывайте о том, что сопротивления могут быть как фиксированными (например, резисторы), так и изменяемыми (потенциометры). При расчетах параллельного сопротивления учитывайте их значения.

Примеры расчетов параллельного сопротивления

Давайте рассмотрим несколько примеров для лучшего понимания расчета параллельного сопротивления.

Пример 1: Два резистора

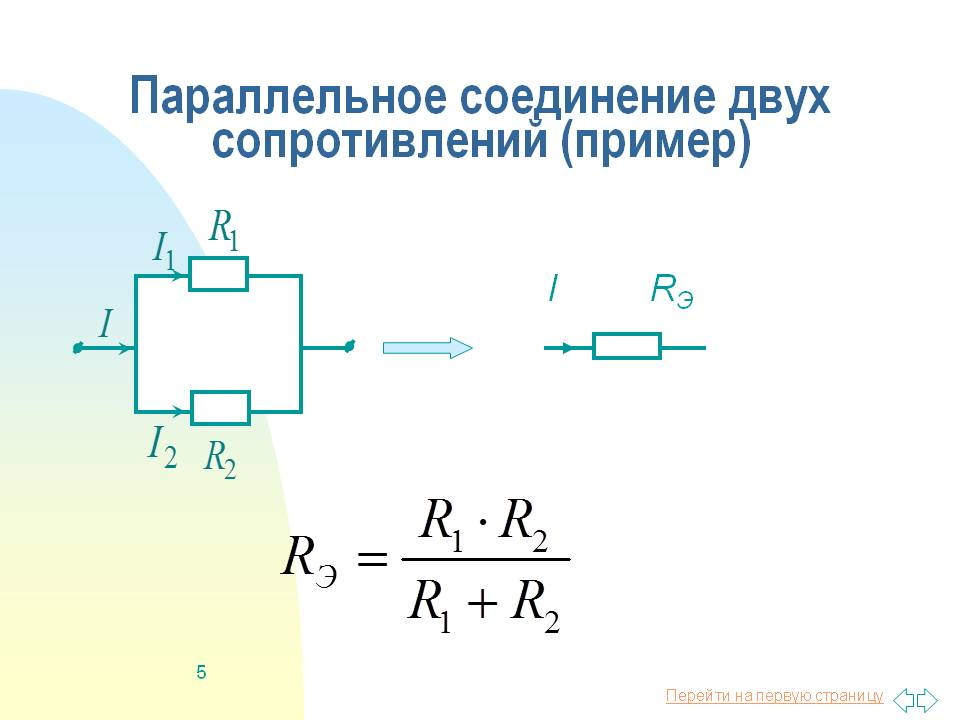
Предположим, у нас есть два резистора: R1 = 100 Ом и R2 = 150 Ом. Давайте найдем их общее параллельное сопротивление.

1. Вычислим обратные величины: 1/R1 = 1/100 Ом = 0.01, 1/R2 = 1/150 Ом ≈ 0.00667.
2. Сложим обратные величины: 0.01 + 0.00667 ≈ 0.01667.
3. Получим обратное от суммы: 1/0.01667 ≈ 60.
4. Получим общее сопротивление: Rпараллельное = 1/60 ≈ 0.0167 Ом.

Пример 2: Три резистора

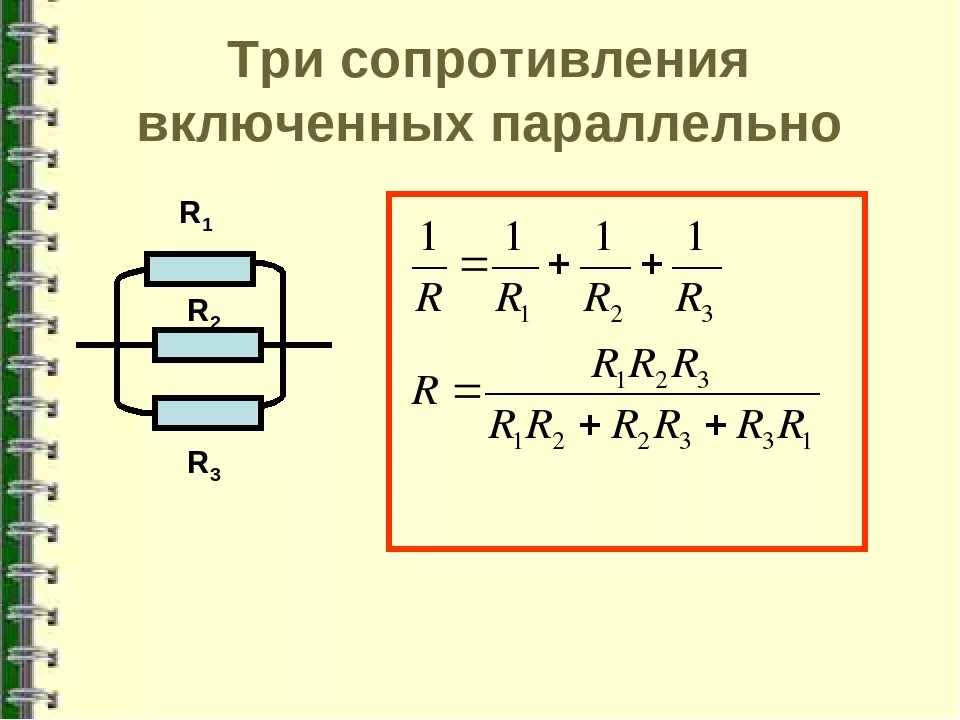
Представим, что у нас есть три резистора: R1 = 200 Ом, R2 = 300 Ом и R3 = 400 Ом. Найдем их общее параллельное сопротивление.

1. Вычислим обратные величины: 1/R1 = 1/200 Ом = 0.005, 1/R2 = 1/300 Ом ≈ 0.00333, 1/R3 = 1/400 Ом ≈ 0.0025.
2. Сложим обратные величины: 0.005 + 0.00333 + 0.0025 ≈ 0.01083.
3. Получим обратное от суммы: 1/0.01083 ≈ 92.18.
4. Получим общее сопротивление: Rпараллельное = 1/92.18 ≈ 0.01085 Ом.

Пример 3: Четыре резистора

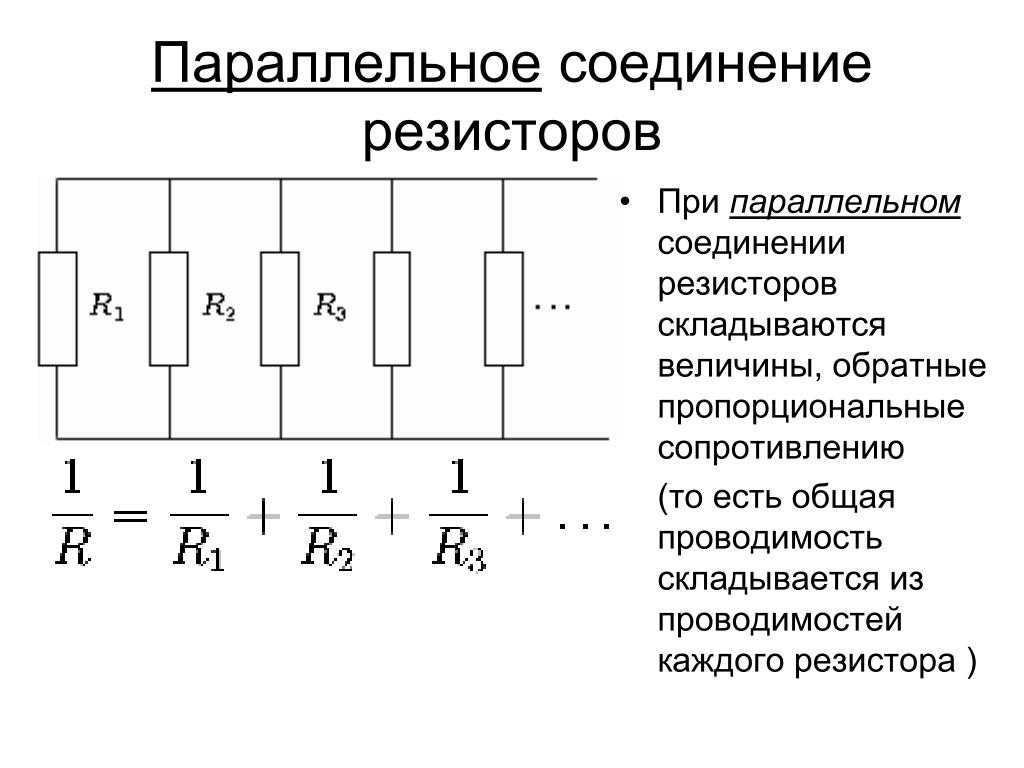
Предположим, у нас есть четыре резистора: R1 = 120 Ом, R2 = 180 Ом, R3 = 240 Ом и R4 = 360 Ом. Найдем их общее параллельное сопротивление.

1. Вычислим обратные величины: 1/R1 = 1/120 Ом ≈ 0.00833, 1/R2 = 1/180 Ом ≈ 0.00556, 1/R3 = 1/240 Ом ≈ 0.00417, 1/R4 = 1/360 Ом ≈ 0.00278.
2. Сложим обратные величины: 0.00833 + 0.00556 + 0.00417 + 0.00278 ≈ 0.02084.
3. Получим обратное от суммы: 1/0.02084 ≈ 48.04.
4. Получим общее сопротивление: Rпараллельное = 1/48.04 ≈ 0.0208 Ом.

В данной статье мы рассмотрели методы расчета параллельного сопротивления в электрических цепях. Мы изучили основные концепции и предоставили примеры для лучшего понимания процесса. Правильное определение параллельного сопротивления является важным навыком при проектировании и анализе электрических систем. С помощью описанных шагов и советов, вы сможете успешно решать задачи, связанные с расчетами сопротивлений в параллельных цепях.