Таблица истинности — это мощный инструмент, который может помочь вам узнать итог логического выражения для возможных его переменных. Изучаете ли вы логику, математику, информатику или любую другую область, научиться создавать такие таблицы — необходимый навык. В этой статье мы расскажем как составить таблицу истинности.
Шаги по созданию таблицы истинности
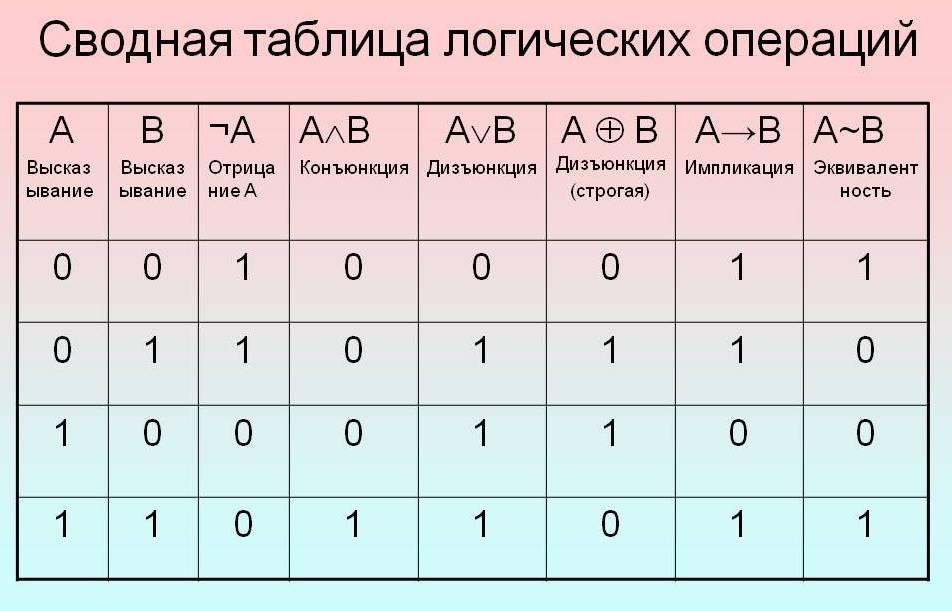
- Перечислите все предложения в высказываниях.
Составление списков. Например, (A и B) или (не C) пропозициями являются A, B и C.
- Определите количество строк
Оно равно 2n, где n — количество предложений в выражении. В нашем примере есть три предложения (A, B и C), поэтому число строк будет равно 2 3 = 8.
- Перечислите все возможные итоги истинности
На этом этапе необходимо перечислить все исходы значений истинности для утверждений внутри выражения. Например, в нашем примере с тремя предложениями (A, B и C) бывает 8 исходов.
- Вычислите значения для всего
В промежутке узнать значение для каждого строкового данного. Для этого вам нужно подставить результаты для предложений в выражении и вычислить пример.
Полезные советы
Начните с простых выражений
Если вы новичок, рекомендуется начать с простых примеров, содержащих только одно или два предложения. Это поможет вам понять, как работают таблицы истинности, прежде чем переходить к более сложным примерам.
Используйте согласованный порядок для предложений
При перечислении предложений в таблице истинности важно использовать согласованный порядок. Это упростит отслеживание того, какое предложение соответствует какому столбцу в таблице.
Используйте таблицу истинности. Для упрощения
Одним из преимуществ является то, что их можно использовать для упрощения сложных логических выражений. Определяя строки в таблице истинности, в которых выражение имеет значение true или false, можно узнать шаблоны, которые можно использовать для упрощения выражения, что позволит вам правильно составить таблицу истинности.
Расширенные концепции в таблицах истинности
Как только вы освоите основы таблиц истинности, вы можете перейти к сложным концепциям. Вот несколько примеров:
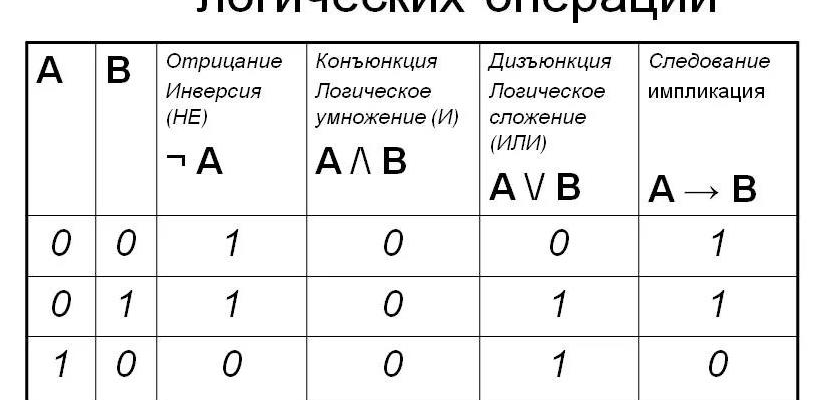
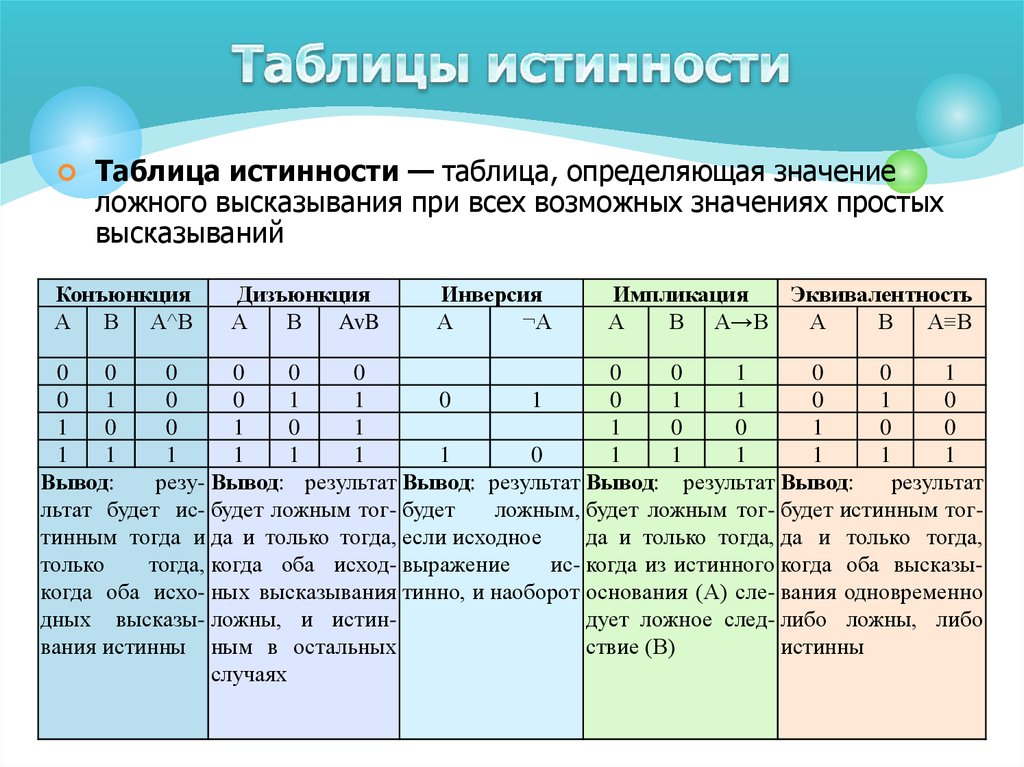
- Отрицание (Инверсия)
Отрицание — это логический оператор, который изменяет смысл предложения на противоположное. В таблице истинности отрицание может быть представлено символом «не» (~).
- Конъюнкция
Это оператор, может быть представлен знаком «и» (&).
- Дизъюнкция
Это оператор, представляющий «или». Она может быть представлена символом «или» (|).
- Условный
Это оператор, который представляет «если-то». В таблице условное обозначение может быть представлено символом стрелки (->).
Следуя нашим советам, вы без труда сможете правильно составить таблицу истинности. А если у вас остались вопросы, задавайте их в комментариях.