Человечество очень долго шло к изобретению первого компьютера. Его созданию способствовали открытия в разных отраслях науки. Помимо технических возможностей, важны были и открытия в области математики. В частности, современные персональные компьютеры и смартфоны, не могли бы функционировать без создания бинарной системы. Почему так часто слышно о 0 и 1 в информатике?
Бинарный язык — это язык, который был создан для выполнения функции установления связи между человеком и машиной. Это важно, потому что без этого языка человек не мог бы контролировать процессы, выполняемые физическими частями компьютера. Помните, что все эти элементы машины состоят из набора электрических частей, которые активируются при пропускании через них тока.
Двоичный язык используется для того, чтобы компоненты аппаратного типа знали, когда им нужно действовать и как они должны действовать. Это очень важно, потому что без этого языка многие физические части компьютера были бы повреждены просто при попытке включить его.
Вопреки видимости, работа компьютерного процессора гораздо менее сложна, чем работа человеческого разума. Процессор различает только два состояния — то, в котором течет ток (1), и то, в котором тока нет (0). На основе этого создаются алгоритмы для гораздо более сложных чисел и общих определенных данных.
Так как же это работает на практике? В двоичной системе 0 — это 0, 1 — это 1, но 10 — это 2, а 11 — это 3. Следуя тому же ходу мыслей, можно заключить, что буква B — это 01100010.
Байт против бита
Единица или ноль — это бит. В свою очередь, восемь таких символов (битов) — это, конечно, один байт. В случае компьютерных значений мы имеем дело с несколько иным коэффициентом преобразования, чем в классической физике. Приставка кило означает, что в одном килобайте не 1000 байт, а 1024 байта.
Конечно, этот несколько иной расчет единиц связан со многими ошибками, которые допускают покупатели компьютерной техники. Многие до сих пор считают, что на терабайтном накопителе может храниться до 1000 гигабайт данных. К счастью, реальность гораздо более благоприятна, чем кажется на первый взгляд.
Кванты вступают в игру

Многие лаборатории работают над квантовыми компьютерами. Чем они отличаются от традиционных компьютеров? Как мы уже упоминали, традиционные компьютеры основаны на системе наличия или отсутствия протекания тока. В квантовом компьютере квант может быть либо единицей, либо нулем. Как это возможно?
Если вспомнить уроки физики, то мы, скорее всего, припомним, что электрон не имеет четко определенного положения по отношению к атомному ядру. Однако можно определить, каково предполагаемое место его нахождения в данный момент (орбита). Это свойство используется современными квантовыми компьютерами или, по сути, их неоперившимися предками.
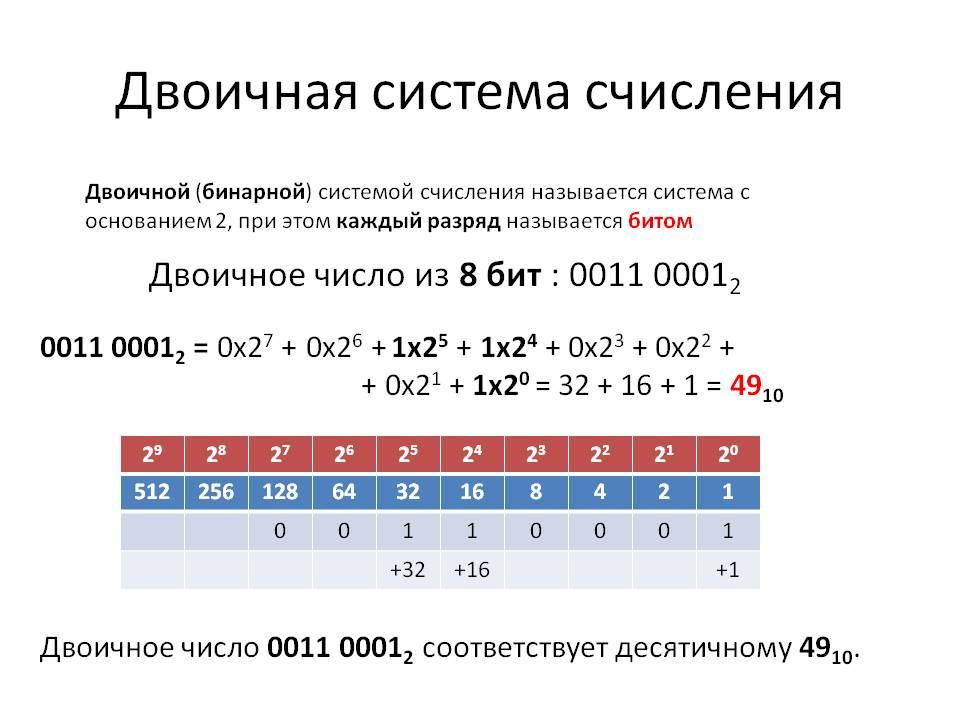
Бинарная или двоичная система счисления
Двоичная система состоит всего из двух цифр: 0 (ноль) и 1 (единица). Она работает так же, как и десятичная система. Возьмем, к примеру, несколько первых чисел нашей десятичной системы. Мы переведем их в двоичную систему, также называемую бинарной. Первое число в нашей системе 0 (ноль). В двоичной системе это число также равно 0, потому что есть такая цифра. Следующее число 1 (один). В двоичной системе такая цифра тоже есть, поэтому пишем 1. Следующее число 2 (два). Мы знаем, что такой цифры нет, поэтому добавляем еще одну позицию и обнуляем позицию справа. Таким образом, число 2 в десятичном виде равно «10» в двоичном. Ни в коем случае не «десять», а «один, ноль». Следующие числа в десятичной системе: 3, 4, 5, 6, 7, 8, 9 и т. д. В двоичной системе они выглядят так: 11, 100, 101, 110, 111, 1000, 1001. Принцип всегда одно и то же. Исходя из этого, становится понятно, сколько цифр в двоичной системе счисления. Цифры всего две, но чисел, зашифрованных ими, может быть сколько угодно, как и букв и иных символов.
Зачем нужны 0 и 1 в информатике?

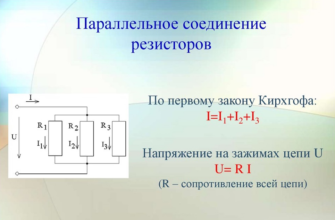
Компьютер состоит из электронных частей. Обмен информацией основан на соответствующей передаче сигналов. Основой электроники является электрический ток, который либо течет, либо не течет в электронных системах. Итак, чтобы компьютеру было легче распознавать сигналы, он интерпретирует протекающий ток как «1» (единица), а его отсутствие — как «0» (ноль). Нетрудно догадаться, что компьютер, работая с соответствующей настройкой, когда по нему течет ток, а когда нет, выставляет разные значения нулей и единиц. Процессор преобразует их в числа и таким образом создаются разборчивые для нас изображения, тексты, звуки и т. д. Нули или единицы могут быть представлены не только в виде электрических сигналов. Также на всех носителях, например на компакт-диске, на котором записывающее устройство прожигает крошечные углубления. Эти впадины — единицы, а «равнины» — нули (или наоборот).

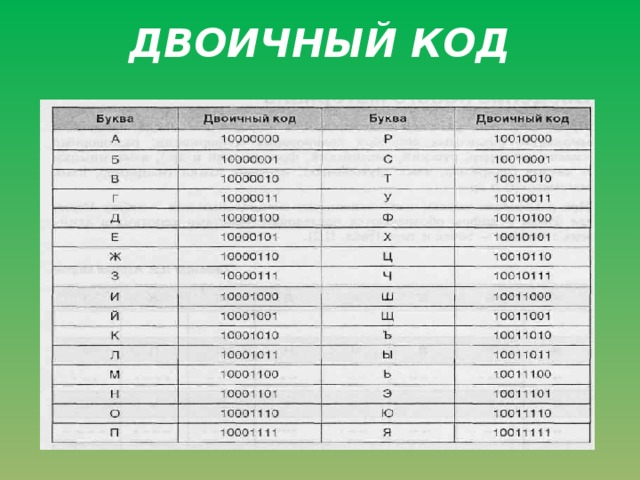
Благодаря двоичному коду стало возможным создать систему ASCII. Эта система имеет большое значение, потому что именно благодаря этой системе мы смогли начать кодировать более сложные программы, выходящие за рамки возможностей, предлагаемых программами, созданными в двоичном коде.
Когда двоичный код входит в физический компонент, он имеет ряд цепей, которые активируются и деактивируются для получения желаемых эффектов. Когда код показывает 1, цепи активируются, а когда он проходит 0, цепи деактивируются. Это создает командную строку, которой может следовать вычислительный блок.
Эти процессы происходят с невероятной скоростью, тысячи и тысячи в секунду.
Преобразование двоичного числа в десятичное
Теперь, когда вы знаете, зачем нам нужна двоичная система, вы узнаете, как преобразовать ее в десятичную систему. Итак, возьмем число, записанное в двоичной системе, например 1000011. Как мы уже говорили, мы начинаем с самых правых (в конце) цифр. Самая правая цифра (в конце) — это число 1, поэтому, как и прежде, умножаем его на основание системы с соответствующей степенью. Все преобразование выглядит следующим образом: 1*2 0 + 1*2 1 + 0*2 2 + 0*2 3 +0*24 + 0*2 5 +1*2 6 , а это равно 1 + 2 + 0 + 0 + 0 + 0 + 64 , поэтому сумма равна 67 десятичной дроби. Вы только что преобразовали двоичное число в десятичное. Теперь было бы хорошо, если бы вы подробно проанализировали приведенную выше конверсию.
Преобразование десятичного числа в двоичное
Обратное преобразование, то есть из десятичного в двоичное число выглядит похожим образом. Сначала мы берем число, которое хотим преобразовать в двоичное. Давайте возьмем число из предыдущего примера и посмотрим, что получиться. Итак, число, которое мы собираемся преобразовать, равно 67. Способ следующий: делим число на 2 и если результат равен: пишем 1, если нет — пишем 0. Затем делим на 2 то, что осталось от числа, но без остатка. Этот процесс продолжается до тех пор, пока не останется 0 (ноль). Полученные нули и единицы записываются в обратном порядке. Это будет объяснено в следующем примере. Сделаем вычисление поэтапно.
1) 67:2 | 1
2) 33:2 | 1
3) 16:2 | 0
4) 8:2 | 0
5) 4:2 | 0
6) 2:2 | 0
7) 1:2 | 1
Что дает 1000011.
Читайте также: Шестнадцатеричная система счисления
Вы также можете видеть, что в самом конце после деления всегда будет 0, поэтому последнее число равно 1. Единица, деленная на два, всегда будет 0,5, поэтому результат с остатком. Следовательно, первая цифра в двоичной системе счисления всегда равна 1. Это можно доказать не только математически. В электронике тоже должно быть так. Мы предположили, что для компьютера отсутствие текущего потока означает «0», а текущий поток — «1». Таким образом, сигнал не может начинаться с «0», потому что это не сигнал (нет напряжения). Процессор не знает, начался ли сигнал уже или его еще нет. Старт должен быть «1» (есть сигнал). Вот почему вы часто слышите про 0 и 1 в информатике.
Кто создал двоичный код?
Это вопрос, который задают многие люди. Это очень важно, потому что открытие этого языка всегда приписывалась только одному человеку на протяжении всей истории.
Если вы знаете историю Исаака Ньютона, вы знаете, что у него был ученый-враг, у которого на самом деле не было злых намерений по отношению к своему коллеге. Этого ученого зовут Готфрид Лейбниц, и его код можно считать проотцом компьютерных технологий.
Именно благодаря Лейбницу сегодня используется именно 0 и 1 в информатике. Это практически единственно возможный путь передачи информации электронным механизмам. Такой язык достаточно сложен для восприятия человеком, но машина способно очень быстро его расшифровать. Для того, чтобы научиться достаточно быстро переводить цифры из десятичной системы в двоичную человеку надо просто потренироваться. Необходимо регулярно рассматривать примеры двоичной системы счисления.
Важность двойной системы заключается в том, что она является основой всех электронных технологий человека. Важно помнить, что бит — это единица измерения виртуального пространства, самая маленькая из всех. Если биты перемножить, то получатся разные шкалы измерения. Многие учитывают это при переводе мегабайтов в гигабиты.